Click a table row,
or a graph point
GERLUMPH
GPU-Enabled, High-Resolution, cosmological MicroLensing parameter survey
GPU-Enabled, High-Resolution, cosmological MicroLensing parameter survey
Centre for Astrophysics and Supercomputing - Swinburne University of Technology
Magnification maps and tools
This is the main GERLUMPH map database, all the publicly available GERLUMPH data can be accessed and analysed here.
Combinations of κ, γ and s parameter values can be selected from the GERLUMPH datasets. Additional map properties e.g. width, resolution, number of lenses, etc, are displayed. Furthermore:
- analyse single or collections of maps by using the tools provided,
- the location in κ,γ parameter space is shown,
- parameter space properties can be viewed as background.
To speed-up the connection we are limiting the query result to 500 maps per query. You can still modify your choice of parameters and select another set of 500 maps.
Number of equivalent maps: Click a table row, Additional data, e.g. light curves, after convolving with different source profiles Click a table row, Download for: Neighbouring macromodels, within Δκ,Δγ = 0.05 Click a table row, |
Select a number of maps from the table on the left,
then click on any tool below.
The maps you have selected will be added to your inventory.
To complete the download, proceed to "checkout".
Inspect the magnification probability distributions (MPDs) of the selected maps.
The "MPD examiner" will open in a new tab.
Maximum limit of 15 maps
All the properties of the selected maps will be listed.
Opens in a new browser tab.
A summary of properties of the selected maps, such as:
computational time, data size, etc.
The maps you have selected by clicking "download" can be accessed here.
Click to proceed with download.
Select a map from the table below,
or click on a point on the plot on the left.
Then use any of the tools on the right.
Preview of the selected map
and its corresponding magnification probability distribution (MPD).
The map can be further inspected using "Colorbar".
Equivalent maps selected within an area of Δκ\',Δγ\' = 0.05.
Transformation from κ,γ,s to κ\',γ\' :
//
$$\kappa^{\prime} = \dfrac{(1-s)\kappa}{1-s\kappa} , \gamma^{\prime} = \dfrac{\gamma}{1-s\kappa}$$
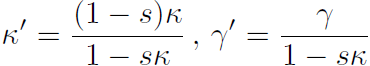
A summary of accretion disc profiles that have been convolved with this map (if available).
Neighbouring κ,γ values from existing macromodels.
Click on the names of the systems to open the "macromodel" tool.
Plot a parameter space property in the background.
An explanation for each background can be found here